Generalized and Scalable Offset-Based Response Time Analysis of Fixed Priority Systems
作者：Deepak Vedha Raj Sudhakar , Karsten Albers, Frank Slomka
固定优先级系统的通用和可扩展的基于偏移的响应时间分析
出处：2021 JSA : Journal of Systems Architecture **，**CCF B类期刊
Keyword: 分模块表现分析（Modular performance analysis )，实时计算(Real-Time Calculus），定时偏移（Timing offsets），到达曲线（Arrival curves ），服务曲线（Service curves ）
原文链接：https://www.sciencedirect.com/science/article/pii/S1383762120301296?via%3Dihub
翻译(基于deepL)：
Abstract:
基于偏移的响应时间分析技术通过考虑任务之间的释放时间依赖性来获得严格的最坏情况响应时间（WCRT）界限。任务或消息的最大响应时间变化（即最坏情况和最佳情况响应时间之间的差异）被用来计算分布式系统的端到端延迟（Palencia和Harbour，1998），（Tindell和Clark，1994）。因此，WCRT评估在确定分布式系统的紧密端到端延迟方面起着重要作用。在实时理论中，存在两种计算任务的WCRT的方法：经典的响应时间分析（RTA）方法和实时计算的模块化性能分析（MPA-RTC）。MPA-RTC起源于网络微积分（NC）。MPA-RTC提供了比基于RTA的技术更强大的抽象，并允许在任务、事件流和资源共享方面进行组合，这使得它成为分析分布式系统的有力候选者（Wandeler, 2006），（Perathoner, 2011）。然而，MPA-RTC的一个关键限制是它不能处理任务之间的偏移依赖，而经典的RTA技术可以处理它们。在本文中，我们提出了一种方法，使用MPA-RTC框架来考虑单处理器系统中固定优先级调度器的任务之间的偏移依赖关系。因此，我们的方法充分利用了MPA-RTC框架模型的优势。我们提出了新的启发式方法和近似方法，以减少基于偏移的RTA的固有复杂性。我们定量评估了我们的方法对最先进的基于偏移的RTA技术的有效性。
Introduction：
在实时系统中，任务或消息是一个可调度的实体，在响应一个定时事件（例如，定时器到期）或接收数据时被激活和执行。任务或消息之间的偏移依赖性确保了一组任务或消息的激活之间有固定的时间间隔，从而避免了同时激活。让我们考虑图1中描述的一个分布式系统的例子。该系统由三个任务𝜏1、𝜏2和𝜏3组成。任务𝜏1的工作完成后会激活任务𝜏2的工作，任务𝜏2的工作完成后会激活任务𝜏3的工作。任务之间的激活依赖关系是借助于偏移量来表达的。因此，在有偏移的系统中，任务的激活之间存在着一种强制的关系。
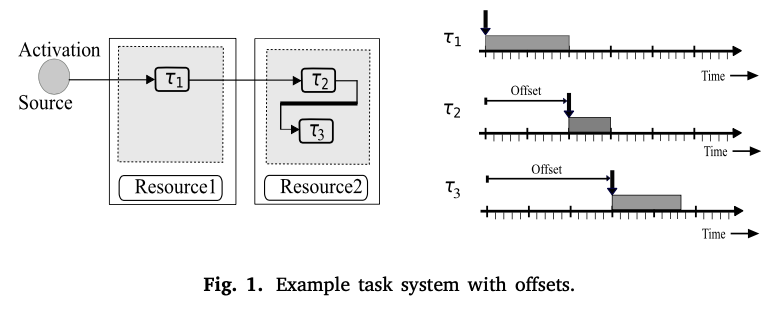
一个任务的激活和完成时间之间所经过的时间等于一个任务的响应时间（图2）。一个任务可能会遇到来自更高优先级任务的干扰，从而延迟该任务的激活工作的完成。一个任务的WCRT等于该任务的激活工作所经历的最长的响应时间。忽视RTA中任务之间的激活依赖关系可能会产生比必要的更多的干扰。因此，有必要将时间偏移纳入计算模型，并扩展RTA以考虑到偏移依赖性。组合式分析框架，如MPA-RTC[1]和SymTA/S[2]将软件任务建模为一个抽象的组件。他们在组件层面上进行分析，单个任务的结果被传播到其他依赖的任务。系统的端到端延迟是通过汇总各个任务的结果得到的。因此，为了计算分布式系统的紧密端到端延迟，必须计算任务的紧密WCRT（见[3,4]）。在图1所示的示例系统中，任务𝜏2的激活抖动取决于任务𝜏1的WCRT。任务𝜏2的WCRT取决于其激活抖动。
如图1所示，任务之间的偏移关系在分布式系统中自然发生。偏移关系在单处理器系统中也被强制执行，因为有几个优点，包括减少输出抖动动作，提高资源利用率，消除资源访问协议（如优先级上限协议），以及增强任务集的可调度性[5-8]。一些实时嵌入式系统使用时间偏移。CAN总线中的一个控制器区域网络（CAN）节点可以传输多个带有偏移的周期性帧。周期性帧流的第一个实例被激活，从一个参考点，即CAN站准备传输的第一个时间点，有一个延迟，称为偏移量[9]。然后定期发送流的后续帧，以第一次传输为时间原点。消息偏移避免了来自同一CAN节点的消息流之间的争夺，并减少了CAN总线的峰值负荷[9,10]。另一个例子是基于AUTOSAR（AUTomotive Open System ARchitecture）[11]的实时操作系统。它使用激活偏移量来避免任务之间的抢占，并确保共享变量之间的数据一致性。基于AUTOSAR的操作系统使用计数器的概念来跟踪反复出现的定时事件（实时时钟刻度）。当计数器达到一个特定值时，AUTOSAR日程表就会过期。过期点被用作衡量一组时间偏移量的参考，每个偏移量被用作触发一组任务的激活源[11]。计划表可以被编程为一次过期或具有循环行为。 存在几种基于偏移量的RTA技术[3,4,12,13]，基于Lehoczky[14]介绍的繁忙期。然而，经典的RTA技术并没有明确地描述可用的处理器容量。经典的RTA技术通过一个迭代过程将可用容量隐含在响应时间方程中。MPA-RTC使用富有表现力的到达曲线对复杂的任务刺激进行建模，并使用服务曲线和抽象的处理组件对不同的调度策略进行建模[1]。MPA-RTC在服务曲线的帮助下明确地描述了可用的处理器能力。然而，MPA-RTC并不考虑任务之间的偏移依赖[1, 15]。在本文中，我们展示了一种在MPA-RTC框架中考虑任务间偏移依赖的通用方法。 一个任务的WCRT计算包括通过识别一组干扰任务的最坏情况下的到达模式来建立一个繁忙期，并计算该任务在繁忙期的间隔内所经历的最大干扰。在没有偏移依赖的系统中，WCRT是通过建立一个繁忙期来获得的，其中一个任务与其他干扰任务模拟释放。该任务和其他干扰任务的连续激活作业会尽快释放。任务的激活工作在繁忙期经历的最长响应时间等于任务的WCRT。对于有任务偏移的系统来说，识别产生任务的WCRT的关键释放瞬间并不是一件简单的事。它导致了一个组合问题，即必须探索不是一个而是几个繁忙期的间隔来确定任务的关键时刻[5,16]。在这项工作中，我们提出了一种可扩展的方法，通过结合启发式方法和近似方法来限制评估的繁忙期间隔的数量。
经典响应时间分析
经典的RTA技术使用Lehoczky[14]提出的i级繁忙期的概念。i级繁忙期被定义为一个处理器忙于执行优先级高于或等于任务𝜏𝑖的任务的最大时间间隔[14]。任务𝜏𝑖的激活作业所经历的WCRT是通过检查i级繁忙期中的几个激活作业获得的（图3）。
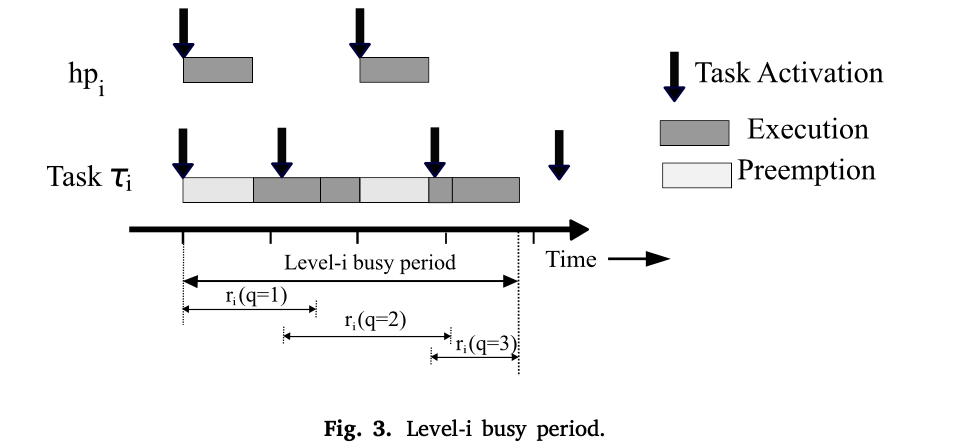
task 𝜏𝑖计算公式：
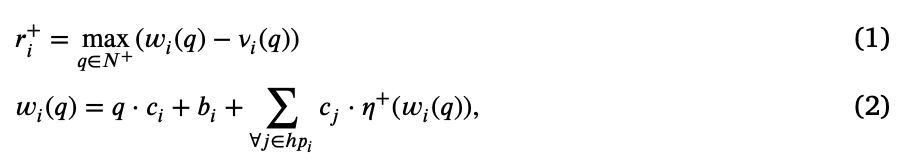
其中
- 𝑤𝑖(𝑞)是任务𝑞的第𝜏𝑖激活工作的完成时间，其中 𝑞∈N+。
- 𝜈𝑖(𝑞)是任务𝑞𝑖的第1次激活作业的激活时间。
- 𝑐𝑖是任务𝜏𝑖的最坏情况下的执行时间。
- 𝑏𝑖是任务𝜏𝑖的最大阻塞时间。
- h𝑝𝑖是一组优先级高于任务𝜏𝑖的任务。
- 𝑛+(𝛥)是任务𝜏𝑖在一个区间内的最大激活作业数。 区间内𝛥的最大激活作业数。
定点迭代一直进行到满足条件𝑤𝑖(𝑞)≤𝜈(𝑞+1)为止，即只要任务𝜏𝑖的连续激活作业(𝑞+1)在任务𝜏𝑖的激活作业完成之前到达。在图3中描述的i级繁忙期，任务𝜏𝑖的第四个激活作业在繁忙窗口𝑤𝑖（𝑞=3）完成后到达。因此，定点迭代收敛于𝑞=3。i级繁忙期（图3）包含任务𝜏𝑖的三个激活作业。WCRT的计算方法是：在第i级繁忙期，三个激活作业所经历的最长响应时间。
使用实时微积分的响应时间分析
实时微积分的模块化性能分析（MPA-RTC）[1]在到达和服务曲线的帮助下进行响应时间分析，它是基于NC[17]。到达曲线是计算需求的模型，服务曲线是任何时间间隔内可用的计算资源的模型。MPA-RTC框架中的任务被建模为一个抽象的组件。MPA-RTC框架能够计算以不同调度策略调度的任务的响应时间，如固定优先级抢占式调度（FPPS）、固定优先级非抢占式调度（FPNS）、时分多址（TDMA）、先进先出（FIFO）和最早期限优先（EDF）[15]。下面，我们描述MPA-RTC中使用的NC的重要特性。NC主要处理一组函数或序列。𝐹, 其中𝐹等于一组非负的广义增加的函数或序列, 如果𝑡<0, 𝑓(𝑡)=0, 并且𝑓(𝑡)∈R+0. 当且仅当∀𝑠≥𝑡，𝑓(𝑠)≥𝑓(𝑡)时，一个函数或序列𝑓被称为广义增加[17]. 𝑓={𝑓(𝑡)}如果参数𝑡∈Z是离散的，则为序列；如果参数𝑡∈R是连续的，则为函数。
定义1. 一个函数或序列𝑓∈𝐹的伪逆𝑓-1定义如下[17]。
𝑓−1(𝑥) = inf{𝑡 ∶ 𝑓(𝑡) ≥ 𝑥}
命题1（水平偏离）。设𝑓和𝑔是𝐹的两个函数或序列。𝐹的两条曲线𝑓和𝑔的图形之间的最大水平偏差可按以下方法计算[17] 。
定义3. 两个函数或序列𝑓和𝑔的最大加权卷积⊗和去卷积⊘定义如下。 两个函数或序列𝑓和𝑔的最大加法卷积⊗和去卷积⊘定义如下。[17]:
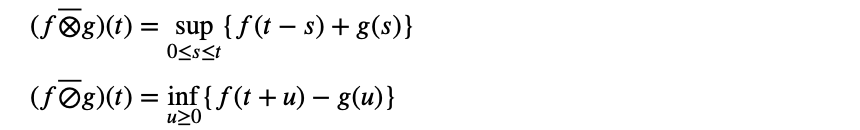事件流描述了触发一个任务的激活工作的事件之间的时间关系。MPA-RTC借助累积到达函数𝑅[𝑢, 𝑣]来表示事件流的轨迹。
定义4. 到达函数𝑅[𝑢, 𝑣)是一个累积函数，表示在时间间隔[𝑢, 𝑣]内到达的事件之和，其中𝑅[𝑢,𝑢]=0，而𝑢，𝑣∈R。 MPA-RTC框架中的事件流被建模为𝛼 = [𝛼l , 𝛼u ]的到达曲线的元组。这些到达曲线代表了一个事件流的所有可能的痕迹。到达曲线的定义如下。
定义5（[1]中的到达曲线定义）。让𝑅[𝑡, 𝑡 + 𝛥)表示在时间间隔[𝑡, 𝑡 + 𝛥)内到达事件流的事件数。那么到达曲线的相应下限𝛼𝑙和上限𝑢满足以下不等式 𝛼𝑙(𝛥)≤𝑅[𝑡,𝑡+𝛥)≤𝛼𝑢(𝛥)∀𝑡∈R, 𝛥∈R+0 （9）与到达函数类似，MPA-RTC 定义了一个服务函数 𝐶[𝑢,𝑣]来描述资源可用性。 定义6. 服务函数𝐶[𝑢,𝑣]是一个累积函数，表示在时间间隔[𝑢, 𝑣]内可用的计算资源单元的总和，其中𝐶[𝑢, 𝑢] = 0，𝑢, 𝑣∈R。 MPA-RTC使用一个服务曲线元组𝛽=[𝛽𝑙,𝛽𝑢]对系统可用的通信和计算资源进行建模。服务曲线的定义如下。 定义7（[1]中的服务曲线定义）。让𝐶[𝑡, 𝑡 + 𝛥]表示在时间区间[𝑡, 𝑡 + 𝛥]内可用的计算资源单位数量。那么，服务曲线的相应下限𝛽𝑙和上限𝛽𝑢满足以下不等式 𝛽𝑙(𝛥)≤𝐶[𝑡,𝑡+𝛥)≤𝛽𝑢(𝛥)∀𝑡∈R, 𝛥∈R+0 （10)。
MPA-RTC借助不同的抽象处理组件来模拟不同的调度策略。根据资源共享方案（调度策略）和抽象处理组件之间的数据流，将所有抽象处理组件的到达和服务输入和输出相互连接，从而得到一个系统模型[1]。一个FIFO和EDF组件分别用于模拟FIFO和EDF调度策略。一个贪婪处理组件（GPC）被用来模拟FPPS和FPNS策略。一个GPC在先进先出的缓冲区中排队接收任务（事件）的激活作业，一旦资源可用，就以贪婪的方式处理激活作业[1]。GPC收到一个到达曲线的元组𝛼 = [𝛼𝑢,𝛼𝑙] 和一个服务曲线的元组𝛽 = [𝛽𝑢, 𝛽𝑙]作为输入，并产生一个传出的到达曲线元组 𝛼′ = [𝛼′𝑢,𝛼′𝑙]和一个传出的服务曲线元组 𝛽 ′ = [𝛽 ′𝑢 , 𝛽 ′𝑙 ] 。MPA-RTC制定了GPC的传递函数，将传入的到达和服务曲线转化为传出的到达和服务曲线。 使用最小加和最大加代数[17]。
接着作者证明了几个Theorem:
GPC转化函数：
任务𝑟𝑖的最坏情况下的响应时间被建模为GPC，其计算方法是：任务𝜏𝑖的上层到达曲线𝑢和下层服务曲线𝑙之间的最大水平偏差。
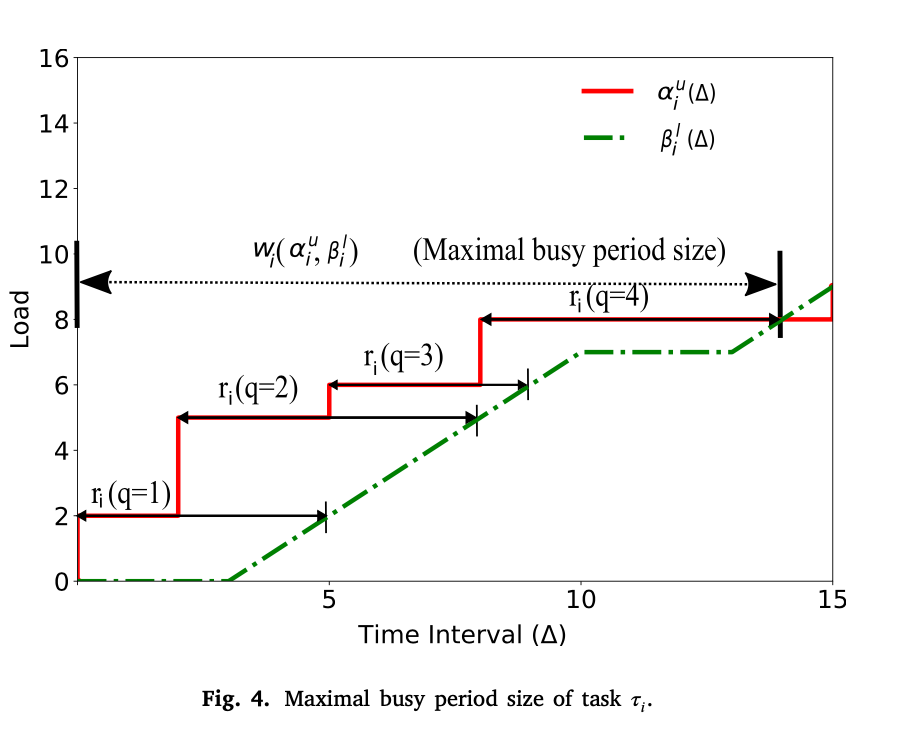
在MPA-RTC中，到达和服务曲线被定义为无限的正实数范围𝛥∈R+0。对于实际实施来说，曲线的有限表示是必要的，而且对曲线的数学运算应该在有限的时间内完成。作品[18,19]使用了曲线的有限表示法，并计算了有限时间间隔内曲线之间的最大水平偏差，称为最大忙碌期大小，即𝑤(𝛼𝑢,𝛽𝑙)（图4）
工作[18,19]表明，对于固定优先级调度策略FPPS和FPNS来说，超过最大繁忙期大小𝑤（𝛼𝑢,𝛽𝑙）的响应时间的计算与系统调度性无关，因此可以忽略。WCRT被计算为激活作业在最大繁忙期尺寸内经历的最大水平偏差，如图4所示。MPA-RTC(公式(16))计算的最大忙时尺寸𝑤(𝛼𝑢,𝛽𝑙)明确考虑了可用服务，而经典的RTA方法(公式(2))则没有考虑。
Related works
基于经典的响应时间分析（RTA）技术
介绍了异步系统
基于网络微积分的技术
介绍了NC和RTA结合以及其他一些NC方面的作品
Paper Contribution
介绍了文章的主要贡献：基于MPA-RTC框架计算时间偏移依赖的WRCT
本文的重点是计算MPA-RTC框架中具有偏移依赖性的任务的WCRT。据我们所知，目前还没有考虑MPA-RTC框架的偏移依赖性的工作。我们解决了第4节中讨论的工作的局限性，以考虑到任意激活抖动的影响。我们为有偏移和激活抖动的任务推导出一套有限的关键到达模式，以执行有效的RTA。第4节中讨论的基于偏移量的RTA技术是难以解决的，其复杂程度是指数级的。尽管存在交易模型的近似和加速技术，但当系统在不同交易的任务之间表现出偏移依赖性时，它们并不适合。我们提出了一种可扩展的基于偏移量的RTA，通过结合启发式和近似式来降低偏移量分析的固有复杂性。
文章结构
本文组织如下：我们在第6节中描述了我们工作中使用的系统模型。在第7节中，我们强调了MPA-RTC方法的局限性和处理偏移依赖关系的复杂性。在第8节中，我们提出了使用MPA-RTC框架为固定优先级调度策略FPPS和FPNS的基于偏移的RTA。在第9节中，我们提出了减少偏移分析的复杂性的技术。在第10节中，我们定量地评估了所提出的方法的有效性，该方法考虑了MPA-RTC框架的偏移量，并与最先进的偏移量分析技术进行了比较。本文在第11节结束。
系统模型
让我们考虑一个固定优先级的抢占式或固定优先级的非抢占式调度器𝛱 ∶= (𝛤,𝛽𝛱𝑙 (𝛥)) 在单处理器上。一组𝑛任务 𝛤 ∶= {𝜏1, 𝜏2, … 𝜏𝑛}被映射到调度器𝛱。这些任务按照优先级顺序编号，最小的数字（索引）被赋予具有最高优先级的任务。任务𝜏1具有最高优先级，任务𝜏𝑛具有最低优先级。我们定义𝛤𝑖 ={𝜏𝑘 ∈𝛤 ∣𝑘∈N，1≤𝑘≤𝑖，𝑛}为具有高于等于任务𝜏（𝜏 ∈𝛤）优先级的任务。在FPPS策略中，如果需要安排一个具有更高优先级的工作，那么正在执行的低优先级工作会被抢占。在FPNS策略中，任务之间不能互相抢占，一个正在执行的工作不会被抢占，即使在其执行期间有更高优先级的工作被请求，也会运行到完成。让𝛽𝛱𝑙（𝛥）对应于调度员𝛱的传入下层服务曲线。它的定义如下。
下层服务曲线（𝛽𝛱𝑙（𝛥））表示调度器𝛱在任何长度为𝛥的时间间隔内所能处理的最小计算需求量[1]。
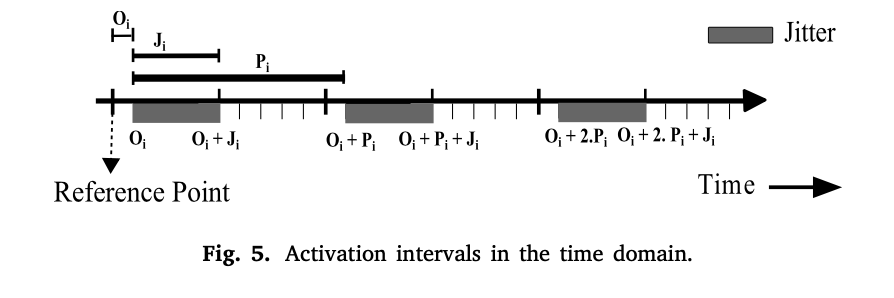
在我们的系统模型中，一个任务𝜏𝑖由一个元组𝜏𝑖 ∶= (𝑐𝑖+ , 𝑑𝑖 , 𝑃𝑖 , 𝑂𝑖 , 𝐽𝑖 ) 表征，其中𝑐𝑖+是该任务的激活作业所要求的最坏情况执行时间（WCET）。𝑑𝑖是任务激活作业的相对期限，参数𝑃𝑖、𝑂𝑖和𝐽𝑖（𝑃𝑖∈N+，𝑂𝑖∈N，𝐽𝑖∈N）指定时间间隔𝐼̂𝑖 i。 e.𝐼̂𝑖 ={[𝑂𝑖+𝑘⋅𝑃𝑖, 𝑂𝑖+ 𝑘⋅𝑃𝑖 + 𝐽𝑖] ∣𝑘∈N}，从固定参考点看，激活任务𝜏𝑖的事件可能发生在这个时间段（图 5）。参数𝑂𝑖等于开始偏移量，代表从固定参考点开始的第一个激活区间。参数𝑃𝑖等于任务𝜏𝑖的激活期，表示间隔的周期性。 参数𝐽𝑖等于任务𝜏𝑖的工作所经历的最大激活抖动，表示间隔的长度。任务𝛼𝑖的上到达曲线𝑢(𝛥)，为一个时间间隔𝛥内的事件数量提供了上限，其获得方法如下[1] 。
基于事件的任务𝜏𝑖的上到达曲线通过将每个事件按WCET（𝑐𝑖+）的比例转换为基于资源的上到达曲线。表1中总结了我们工作中的重要记号。
Problem formulation
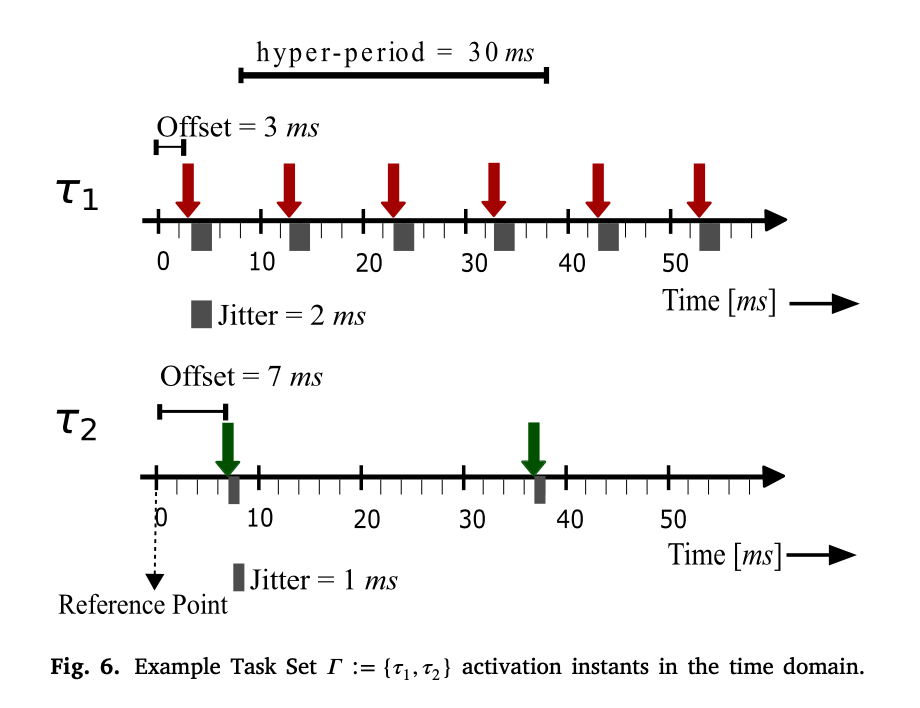
我们考虑一个固定优先级的抢占式调度器𝛱，其传入的下层服务曲线𝛽𝛱𝑙（𝛥）使用MPA-RTC框架建模，如图7所示。调度器𝛽𝛱𝑙（𝛥）的传入服务曲线𝛱为TDMA资源上一个周期为30ms、时隙大小为28.5ms的时隙的资源可用性（下限）。一个由两个任务{𝜏1 , 𝜏2 }组成的任务集𝛱被映射到调度器，其中𝜏1 = （2 ms,5 ms,10 ms,3 ms,2 ms），𝜏2 = （3 ms, 6 ms, 30 ms, 7 ms, 1 ms）。任务𝜏1和任务𝜏2从固定参考点的激活间隔如图6所示。
MPA-RTC用一个GPC链来模拟一个FPPS策略，如图7所示。任务集𝛤中的任务被建模为一个GPC。任务𝜏1的传入下限服务曲线等于调度器的传入下限服务，即𝛽1𝑙（𝛥）= 𝛽𝛱（𝛥）。𝛼1𝑢 , 𝛼2𝑢代表任务𝜏1和𝜎1的上层到达曲线。
任务𝜏2，用公式（16）得到。𝛽 ′𝑙 , 𝛽 ′𝑙代表任务𝜏1和任务𝜏2的出局下层服务曲线。一个任务的出站下限服务是用公式（14）计算的。服务曲线的传播反映了FPPS策略中任务的优先级[15]。低优先级的任务𝜏2只得到高优先级任务𝜏1留下的处理资源。因此，任务𝜏1的出站低服务曲线，即𝛽′𝑙被作为入站低服务曲线提供给下一个低优先级任务 任务𝜏2（图7)。任务集中的任务的上层到达曲线和下层服务曲线 任务集𝛤中的任务的传入上层到达曲线和下层服务曲线显示在图7。
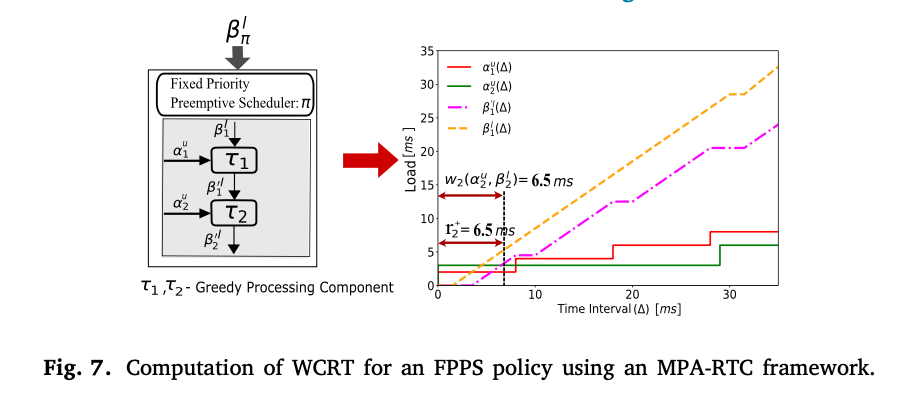
为了计算任务𝜏2的WCRT，使用公式（16）确定最大的繁忙期大小，即𝑤（𝛼2𝑢 ，𝛽2𝑙）为6.5ms（图7）。在区间𝑤(𝛼2𝑢 , 𝛽2𝑙)内的最大水平偏差对应于任务𝜏2的WCRT[18,19]。如图7所示，任务𝜏2的WCRT被计算为6.5ms。
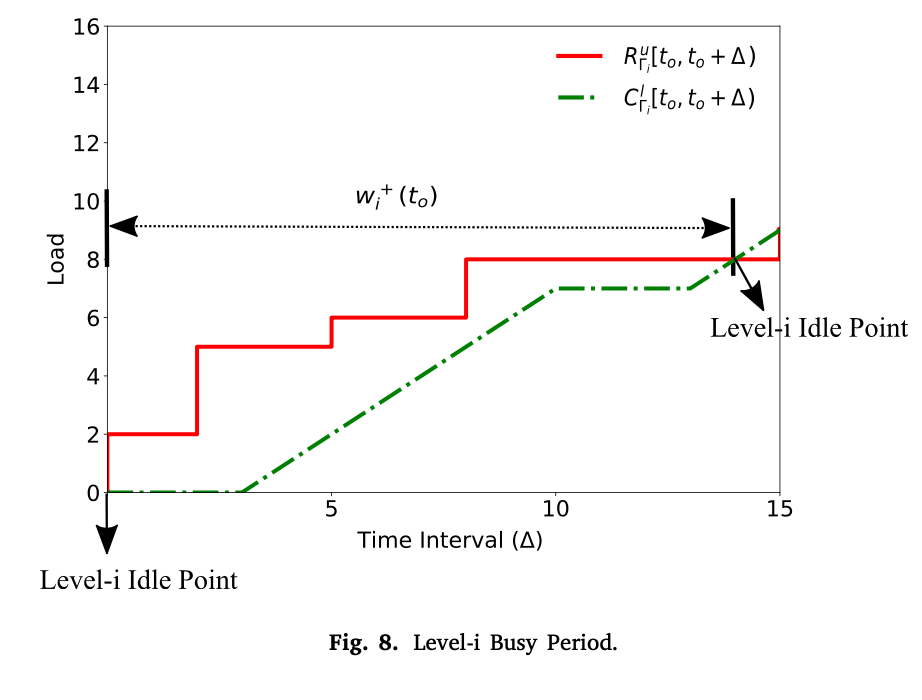
定义9. 一个i级空闲点是一个时间瞬间𝑡𝑜，在这个时间点上，每个在𝑡𝑜之前发布的、优先级高于或等于i的作业在时间𝑡𝑜之前已经完成[36]。 定义10. 一个i级繁忙期是指两个连续的i级空闲点之间长度不为零的时间间隔[𝑡𝑜,𝑡𝑜+𝛥], 在这个时间间隔内只有优先级高于或等于i的作业被处理, 其中𝛥∈R>0[36]. 定义11（AggregateUpperArrivalFunction）。让我们定义𝑅𝑢𝛤𝑖 [𝑡𝑜, 𝑡𝑜 + 𝛥）作为一个聚合上到达函数，表示集合𝛤𝑖中的所有任务在一个时间间隔[𝑡𝑜 , 𝑡𝑜 + 𝛥）内要求的最大累积执行需求。 定义12（聚合下限服务函数）。让我们定义𝐶𝛤𝑙 [𝑡𝑜,𝑡𝑜 + 𝛥）作为一个聚合的下层服务函数，表示在一个时间间隔内[𝑡𝑜 , 𝑡𝑜 + 𝛥），可用于处理集合𝛤𝑖中所有任务激活作业的计算资源单元的最小数量。
如图8所示，一个i级繁忙期间隔的开始和结束由i级空闲点标记。 根据定义10，我们可以推断，任务𝜏𝑖的WCRT发生在由任务𝜏𝑘激活作业启动的i级繁忙期之一（𝜏𝑘∈ 𝛤𝑖）。让我们考虑实例任务集𝛤的超周期区间[3 ms, 33 ms]。引起任务𝜏2的二级繁忙期的潜在二级空闲点是{3 ms,4 ms,5 ms,7 ms,8 ms,13 ms,14 ms,15 ms,23 ms, 24 ms,25 ms}中的一个值。上述集合中的每一个潜在的二级空闲点都对应于超时期内任务的独特到达模式。因此，对于一个有两个任务的简单任务集，需要探索的潜在忙碌期的数量等于11。潜在繁忙期的数量随着任务数、抖动和超期的增加而呈指数级增长。因此，我们需要一种有效的方法来限制带有偏移和抖动的任务的关键到达模式的数量，以实现一个可操作的基于偏移的RTA。
基于偏移的响应时间分析
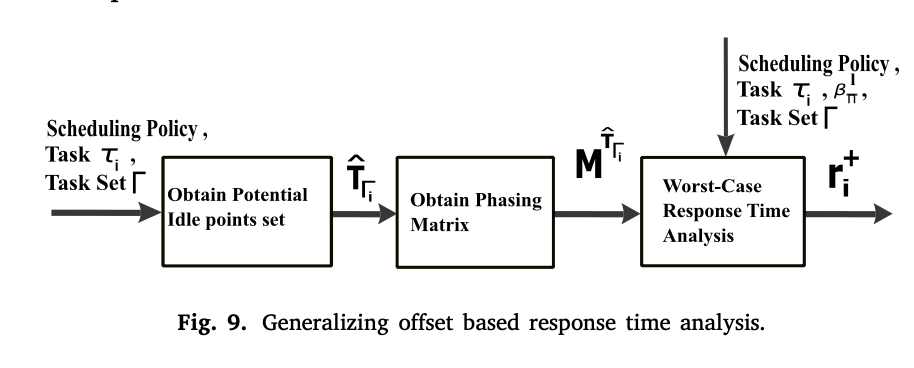
在这一节中，我们详细描述了为固定优先级调度策略泛化基于抵消的RTA所涉及的一系列步骤（图9）。我们的方法包括以下几个步骤。 (1) 我们确定一个减少的潜在i级空闲点集合，启动一个i级繁忙期，可能会引起任务𝜏𝑖的WCRT。 (2) 在相位矩阵的帮助下，捕获对应于潜在i级空闲点集合的独特到达模式。 (3) 我们利用相位信息、调度策略类型和可用容量建立了一组最大的i级繁忙期。 (4) 我们从一组潜在的最大级别i繁忙期中获得被分析任务的激活工作所经历的WCRT。
减少系统复杂度
- 通过启发式方法减少相位矩阵
相位矩阵𝑀𝑇̂𝛤𝑖包含在集合𝑇̂的每个测试点计算的相位向量集合。然而，并不是所有的相位向量都能促成最坏情况下的行为。
- 近似法
确定一组具有抵消依赖性的任务的可行性是一个NP-hard问题[16]。因此，使用启发式方法作为降低复杂性的唯一方法是不够的。通过丢弃任务之间的依赖关系，并将偏移依赖关系限制在一个较小的集合中，偏移分析的复杂性会大大降低，因为它导致了超周期的减少[16]。任务𝜏1和任务𝜏2在固定偏移和固定抖动下发布的激活作业之间的最小时间间隔在[0, 𝐺𝐶 𝐷(𝑃1 , 𝑃2 )]的范围内。(定理3)。如果任务周期𝑃1和𝑃2是相对质数，则𝐺𝐶𝐷(𝑃1 , 𝑃2 )的值为1，任务𝜏1和𝜏2的激活作业之间的最小时间间隔等于0。在本节中，我们提出了一种新颖的近似方法，通过考虑任务集𝛤𝑖中一组周期的共同质数，而不是随机丢弃任务，来限制依赖关系。
通过近似，我们限制了测试点并使偏移分析变得可行。由于近似可能导致悲观的最坏情况下的界限，因此最好设计一个灵活的近似因子来调整运行时间和分析的精确性之间的权衡。我们引入了一个近似系数𝛬（𝛬∈N+），作为偏移分析所考虑的测试点（i级繁忙期）数量的上限。因此，测试点的数量由任务集𝛤 𝑟贡献的测试点数量受到近似系数𝛬的限制。如果𝛬 ≥ |𝑇̂ |，则任务集𝛤𝑖中的所有𝛤任务都被设定为一个值。任务集𝛤𝑖中的任务被加入到𝛤𝑟集中。然而，对于近似系数被设定为一个值即𝛬 < |𝑇̂𝛤𝑖的情况，有必要从𝛤𝑖中选择一个任务子集附加到任务集𝛤𝑟，并确保为偏移分析考虑的测试点数量受到上限𝛬限制。
实验验证
在这一节中，我们定量地评估了第9节中讨论的降低复杂性技术的有效性。我们在chronVAL[38]中实现了所提出的方法，这是INCHRON ToolSuite[39]中的一个形式化时序分析工具。chronVAL使用MPA-RTC框架来确定实时嵌入式系统的最坏情况界限。最先进的基于偏移的RTA技术没有考虑到任意传入的服务。相比之下，我们的计算模型和基于偏移的RTA能够考虑到任意传入的服务曲线。然而，为了与经典的基于偏移的RTA技术进行比较，我们考虑一个完全专用的单处理器，使用FPPS策略来安排任务。
作者对比了几个前人的实验，并在自己提出的方法进行了比较
实验结果表明：
我们的方法比其他技术计算出更好的WCRT界限。我们的方法即使在利用率高达 𝑈=0.8的系统中也能得到非常高的调度性比率。在任务数𝑛=500的情况下，不考虑偏移的MPA-RTC认为没有一个任务集可以调度，Redell-RTA方法认为2000个任务集中有1368个任务集可以调度，而我们的方法认为2000个任务集中有1982个任务集可以调度。我们的方法比MPA-RTC的可调度性提高了约99.1%，而比Redell-RTA的可调度性提高了约30.7%。产生的任务系统具有较大的抖动分布[0 ; 0.2 𝑃]。因此，在Redell-RTA中，抖动对响应时间的贡献更加显著，导致高估了。我们的方法，尽管有近似值（𝛬=500），但计算出的界限比Redell-RTA更好。传统的MPA-RTC计算出的响应时间与传统的关键时刻的概念相符，假设所有的任务都是同步发布的。由于我们使用提议的带有偏移考虑的MPA-RTC克服了这一限制，我们的方法在现实的工业任务集上明显优于没有偏移考虑的传统MPA-RTC。
总结和展望
在本文中，我们提出了一种新的方法，使用基于MPA-RTC的系统模型来考虑固定优先级系统的偏移-挂起。我们在超时空内确定了一组潜在的i级空闲点，这些空闲点会对所分析的任务产生最坏情况下的干扰，并确定了WCRT。此外，我们提出了限制超周期内任务的关键到达模式的方法，以解决基于抵消的RTA的复杂性问题。我们通过一系列实验表明，我们的方法极大地提高了任务集的可调度性，并且在一个真实世界的汽车基准中优于最先进的RTA技术。我们通过使用具有大的和小的超周期的任务集进行实验，说明了我们的方法比其他最先进的基于偏移的RTA技术的可扩展性。 在我们的计算模型中，我们考虑了带有偏移和抖动的周期性事件模型，并借助元组（𝑃,𝑂,𝐽）来表示潜在的激活间隔。然而，我们的方法可以扩展到考虑其他事件模型，如突发事件[40]，方法是将元组（𝑃,𝑂,𝐽）扩展到类似于Gresser事件模型的元组集合[41]。将我们的偏移分析整合到分布式系统的更大的MPA-RTC分析框架中，以及对出站流量的编译，将在我们未来的工作中讨论。