商务智能课堂笔记,对这一部分比较感兴趣。
看PDF应该是老师和百度有合作,内容都是PaddlePaddle提供的。

作业 记录
1. *请说明描述性分析、 预测性分析、 规范性分析的含义,并采用一个综合例子说明这三种分析的应用。(**12**分)*
描述性分析:描述已经发生了什么。它是对历史的洞察,即回答“发生了什么?”。描述性分析使用简单的数学和统计方法就能实现,典型的分析指标例如计数、均值、中位数、众数、方差、分布、相关系数等。
预测性分析:预测将会发生什么。预测性分析大多是基于概率的,即预测事件在未来发生的概率,或者事件在大概率上会如何发生。在预测性分析中,使用了多种技术,例如数据挖掘,统计建模和机器学习算法(分类,回归和聚类技术)等等,它最终的目的是试图预测可能的未来结果并提供这些结果发生的可能性。
规范性分析:提供应该怎么办的建议。规范性分析吸收描述性分析与预测性分析中的结论,通过为企业推荐最佳的可行方案来得到行动建议
例子:比如一家短视频公司需要分析用户的视频喜好,从未为用户推荐更多他们喜爱的短视频类型。
使用描述性分析,分析用户在平台上观看短视频的数据,计算方差,均值,还有一些相关系数:年龄和视频类型的相关系数,性别和视频类型的相关系数等。
使用预测性分析:将拿到的数据进行分类,回归,聚类等其他机器学习算法,或者将数据投喂给深度学习模型,从而实现预测,比如拿到用户的性别年龄,过往喜好来预测用户对哪些短视频更有兴趣。
使用规范性分析:根据用户的这种偏好,平台怎么调整自己的策略来让用户对产品的粘性更高。比如把更多用户偏好的短视频推荐给他们,把与之相关的广告更精准推荐给他们。
2. *请描述数据挖掘的步骤,请简述每个步骤的基本含义。(**10**分)*
步骤(1)*信息收集*:根据确定的数据分析对象,抽象出在数据分析中所需要的特征信息,然后选择合适的信息收集方法,将收集到的信息存入数据库。对于海量数据,选择一个合适的数据存储和管理的数据仓库是至关重要的。
步骤(2)*数据集成*:把不同来源、格式、特点性质的数据在逻辑上或物理上有机地集中,从而为企业提供全面的数据共享。
步骤(3)*数据规约*:如果执行多数的数据挖掘算法,即使是在少量数据上也需要很长的时间,而做商业运营数据挖掘时数据量往往非常大。数据规约技术可以用来得到数据集的规约表示,它小得多,但仍然接近于保持原数据的完整性,并且规约后执行数据挖掘结果与规约前执行结果相同或几乎相同。
步骤(4)*数据清理*:在数据库中的数据有一些是不完整的(有些感兴趣的属性缺少属性值)、含噪声的(包含错误的属性值),并且是不一致的(同样的信息不同的表示方式),因此需要进行数据清理,将完整、正确、一致的数据信息存入数据仓库中。不然,挖掘的结果会差强人意。
步骤(5)*数据变换*:通过平滑聚集、数据概化、规范化等方式将数据转换成适用于数据挖掘的形式。对于有些实数型数据,通过概念分层和数据的离散化来转换数据也是重要的一步。
步骤(6)*数据挖掘过程*:根据数据仓库中的数据信息,选择合适的分析工具,应用统计方法、事例推理、决策树、规则推理、模糊集,甚至神经网络、遗传算法的方法处理信息,得出有用的分析信息。
步骤(7)*模式评估*:从商业角度,由行业专家来验证数据挖掘结果的正确性。
步骤(8)*知识表示*:将数据挖掘所得到的分析信息以可视化的方式呈现给用户,或作为新的知识存放在知识库中,供其他应用程序使用。
3. *请**编写程序实现**A**priori**算法**和**FP**-**G**rowth**算法,算法**可以根据**给定**的支持度和置信度获取所有的频繁项集**和**关联规则。**请自拟数据集进行测试。(2**5**分)*
Apriori算法:
核心代码:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
def loadDataSet():
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
#发现频繁项集
def createC1(dataSet):
C1=[]
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item])
C1.sort()
return list(map(frozenset,C1))
def scanD(D,CK,minSupport):
ssCnt = {}
for tid in D:
for can in CK:
if can.issubset(tid):
if not can in ssCnt:ssCnt[can]=1
else:ssCnt[can]+=1
numItems = float(len(D))
retList = []
supportData={}
for key in ssCnt:
support = ssCnt[key]/numItems
if support>=minSupport:
retList.insert(0,key)
supportData[key]=support
return retList,supportData
#频繁项集两两组合
def aprioriGen(Lk,k):
retList=[]
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1,lenLk):
L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
L1.sort();L2.sort()
if L1==L2:
retList.append(Lk[i]|Lk[j])
return retList
# 最小支持度域值设置为0.5
def apriori(dataSet,minSupport=0.7):
C1=createC1(dataSet)
D=list(map(set,dataSet))
L1,supportData =scanD(D,C1,minSupport)
L=[L1]
k=2
while(len(L[k-2])>0):
CK = aprioriGen(L[k-2],k)
Lk,supK = scanD(D,CK,minSupport)
supportData.update(supK)
L.append(Lk)
k+=1
return L,supportData
# 找关联规则
# 规则计算的主函数
def generateRules(L,supportData,minConf=0.5):
bigRuleList = []
for i in range(1,len(L)):
for freqSet in L[i]:
H1 = [frozenset([item]) for item in freqSet]
if(i>1):
rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
else:
calcConf(freqSet,H1,supportData,bigRuleList,minConf)
return bigRuleList
def calcConf(freqSet,H,supportData,brl,minConf=0.5):
prunedH=[]
for conseq in H:
conf = supportData[freqSet]/supportData[freqSet-conseq]
if conf>=minConf:
print (freqSet-conseq,'--->',conseq,'conf:',conf)
brl.append((freqSet-conseq,conseq,conf))
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):
m = len(H[0])
if (len(freqSet)>(m+1)):
Hmp1 = aprioriGen(H,m+1)
Hmp1 = calcConf(freqSet,Hmp1,supportData,brl,minConf)
if(len(Hmp1)>1):
rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)
if __name__=='__main__':
dataSet=loadDataSet()
L,supportData=apriori(dataSet)
rules = generateRules(L,supportData,minConf=0.5)
拟定数据:
[1,3,4],[2,3,5],[1,2,3,5],[2,5]
最小支持度设置为0.5,最小置信度设置为0.7时,测试结果:

修改最小支持度和最小置信度,分别修改为0.7和0.5,测试结果:

Fp-growth算法
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
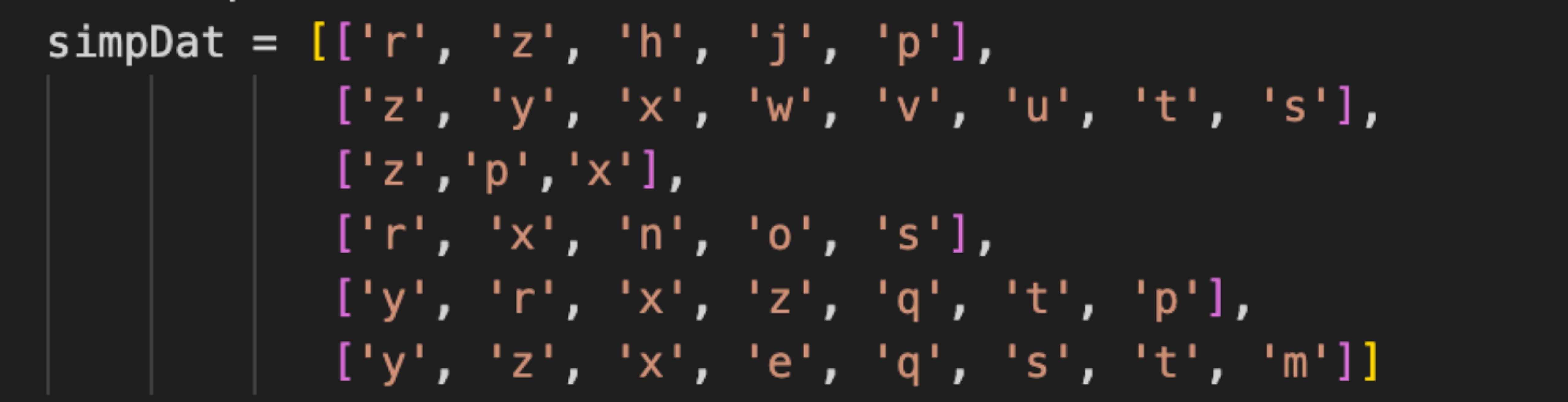
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z','p','x'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
class treeNode:
def __init__(self, nameValue, numOccur, parentNode):
self.name = nameValue
self.count = numOccur
self.nodeLink = None
self.parent = parentNode #needs to be updated
self.children = {}
def inc(self, numOccur):
self.count += numOccur
def disp(self, ind=1):
print ((' '*ind, self.name, ' ', self.count))
for child in self.children.values():
child.disp(ind+1)
def createTree(dataSet, minSup=1): #create FP-tree from dataset but don't mine
headerTable = {}
#go over dataSet twice
for trans in dataSet:#first pass counts frequency of occurance
for item in trans:
headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
for k in list(headerTable.keys()): #remove items not meeting minSup
if headerTable[k] < minSup:
headerTable.pop(k)
freqItemSet = set(headerTable.keys())
#print 'freqItemSet: ',freqItemSet
if len(freqItemSet) == 0: return None, None #if no items meet min support -->get out
for k in headerTable:
headerTable[k] = [headerTable[k], None] #reformat headerTable to use Node link
#print 'headerTable: ',headerTable
retTree = treeNode('Null Set', 1, None) #create tree
for tranSet, count in dataSet.items(): #go through dataset 2nd time
localD = {}
for item in tranSet: #put transaction items in order
if item in freqItemSet:
localD[item] = headerTable[item][0]
if len(localD) > 0:
orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
updateTree(orderedItems, retTree, headerTable, count)#populate tree with ordered freq itemset
return retTree, headerTable #return tree and header table
def updateTree(items, inTree, headerTable, count):
if items[0] in inTree.children:#check if orderedItems[0] in retTree.children
inTree.children[items[0]].inc(count) #incrament count
else: #add items[0] to inTree.children
inTree.children[items[0]] = treeNode(items[0], count, inTree)
if headerTable[items[0]][1] == None: #update header table
headerTable[items[0]][1] = inTree.children[items[0]]
else:
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
if len(items) > 1:#call updateTree() with remaining ordered items
updateTree(items[1::], inTree.children[items[0]], headerTable, count)
def updateHeader(nodeToTest, targetNode): #this version does not use recursion
while (nodeToTest.nodeLink != None): #Do not use recursion to traverse a linked list!
nodeToTest = nodeToTest.nodeLink
nodeToTest.nodeLink = targetNode
def ascendTree(leafNode, prefixPath): #ascends from leaf node to root
if leafNode.parent != None:
prefixPath.append(leafNode.name)
ascendTree(leafNode.parent, prefixPath)
def findPrefixPath(basePat, treeNode): #treeNode comes from header table
condPats = {}
while treeNode != None:
prefixPath = []
ascendTree(treeNode, prefixPath)
if len(prefixPath) > 1:
condPats[frozenset(prefixPath[1:])] = treeNode.count
treeNode = treeNode.nodeLink
return condPats
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
bigL = [k for k,v in sorted(headerTable.items(), key=lambda p: p[1][0])]#(sort header table)
for basePat in bigL: #start from bottom of header table
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
#print 'finalFrequent Item: ',newFreqSet #append to set
freqItemList.append(newFreqSet)
condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
#print 'condPattBases :',basePat, condPattBases
#2. construct cond FP-tree from cond. pattern base
myCondTree, myHead = createTree(condPattBases, minSup)
#print 'head from conditional tree: ', myHead
if myHead != None: #3. mine cond. FP-tree
#print 'conditional tree for: ',newFreqSet
#myCondTree.disp(1)
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
def createInitSet(dataSet):
retDict = {}
for trans in dataSet:
retDict[frozenset(trans)] = 1
return retDict
minSup = 4
simpDat = loadSimpDat()
initSet = createInitSet(simpDat)
myFPtree, myHeaderTab = createTree(initSet, minSup)
myFreqList = []
if myFPtree is not None:
myFPtree.disp()
mineTree(myFPtree, myHeaderTab, minSup, set([]), myFreqList)
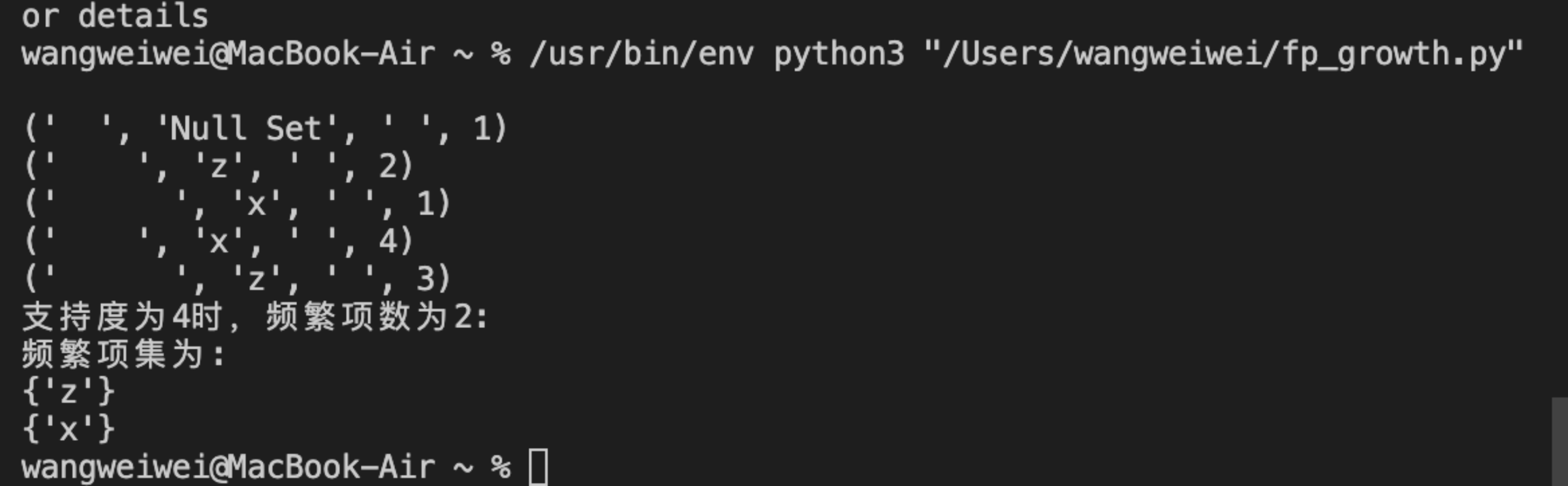
print("支持度为%d时,频繁项数为%d:"%(minSup, len(myFreqList)))
print("频繁项集为:")
for item in myFreqList:
print(item)
测试数据:
测试结果:
代码运行环境:python3.7
完整代码见 ./压缩包/代码
\4. 请编写程序实现决策树算法,请自拟数据集进行测试。(20分)
核心代码:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from math import log
def createDataSet():
#outlook:sunny:1,overcast:2,rainy:3
#temperature:hot:1,mild:2,cool:3
#humidity:high:1,normal:2
#windy:false:1,true:2
#play:no,yes
dataSet=[
[1,1,1,1,'no'],
[1,1,1,2,'no'],
[2,1,1,1,'yes'],
[3,2,1,1,'yes'],
[3,3,2,1,'yes'],
[3,3,2,2,'no'],
[2,3,2,2,'yes'],
[1,2,1,1,'no'],
[1,3,2,1,'yes'],
[3,2,2,1,'yes'],
[1,2,2,2,'yes'],
[2,2,1,2,'yes'],
[2,1,2,1,'yes'],
[3,2,1,2,'no']
]
labels=['outlook','temperature','humidity','windy','play']
return dataSet,labels
def calcShannonEnt(dataSet):
#返回数据集行数
numEntries=len(dataSet)
#保存每个标签(label)出现次数的字典
labelCounts={}
#对每组特征向量进行统计
for featVec in dataSet:
currentLabel=featVec[-1]#提取标签信息
if currentLabel not in labelCounts.keys():#如果标签没有放入统计次数
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1#label计数
shannonEnt=0.0
#计算经验熵
for key in labelCounts:
prob=float(labelCounts[key])/numEntries #选择该标签的概率
shannonEnt-=prob*log(prob,2) #利用公式计算
return shannonEnt
def chooseBestFeatureToSplit(dataSet):
#特征数量
numFeatures = len(dataSet[0]) - 1
#计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
#信息增益
bestInfoGain = 0.0
#最优特征的索引值
bestFeature = -1
#遍历所有特征
for i in range(numFeatures):
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
#创建set集合{},元素不可重复
uniqueVals = set(featList)
#经验条件熵
newEntropy = 0.0
#计算信息增益
for value in uniqueVals:
#subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
#计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
#根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet))
#信息增益
infoGain = baseEntropy - newEntropy
#打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
#计算信息增益
if (infoGain > bestInfoGain):
#更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
#记录信息增益最大的特征的索引值
bestFeature = i
#返回信息增益最大特征的索引值
return bestFeature
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
if __name__=='__main__':
dataSet,features=createDataSet()
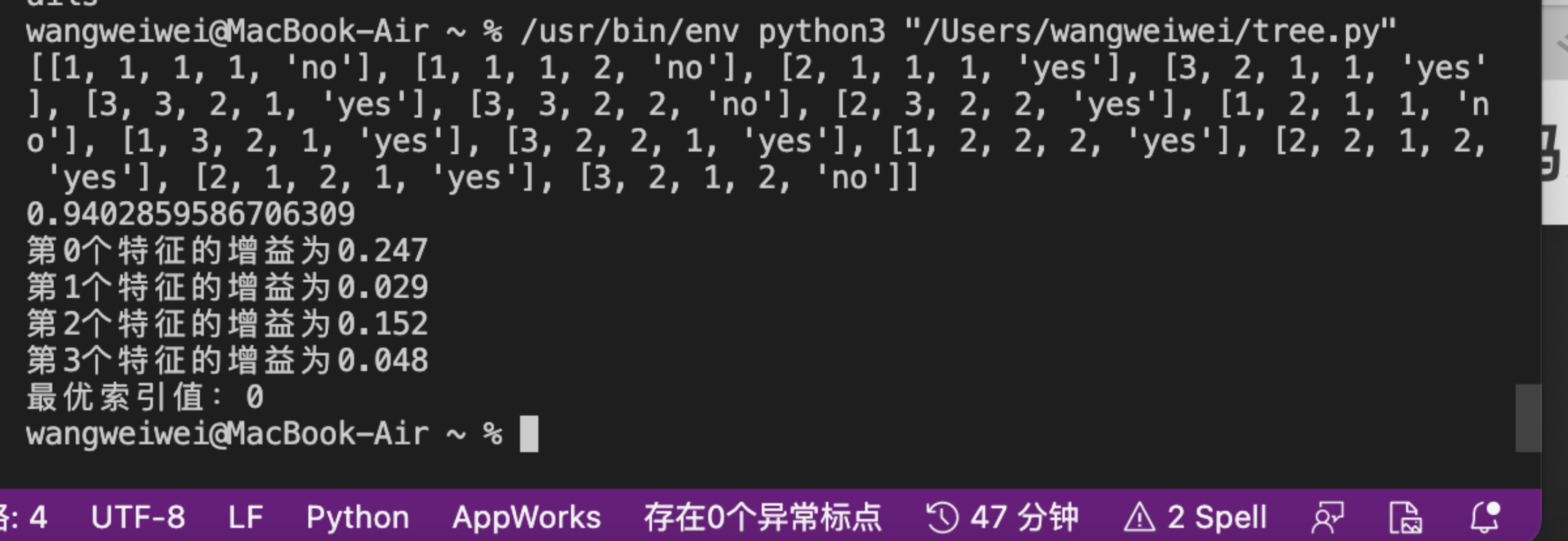
print(dataSet)
print(calcShannonEnt(dataSet))
print("最优索引值:"+str(chooseBestFeatureToSplit(dataSet)))
测试结果:
5. *请分析k**-means**算法和k中心点算法的异同。(**8**分)*
相同之处:
在第一步:选择k个随机的点作为初始的种子点和第二步:针对每个簇中,随机在选一个点为新的种子点构建新的划分,k-means算法和k中心点算法没有区别,是相同的。
第五步两者都是重复计算E的值直到没有能够使得E值更小的划分为止。
不同之处:
在第三步,k-means对簇中的点求均值,均值可能并不存在于簇中,k中心点算法采用的是在簇中随机的点作为新种子,再构建新的划分,新种子一点是真实存在簇中。
第四步:计算距离时公式不同:k-中心点中的dist(p,ci)没有平方。
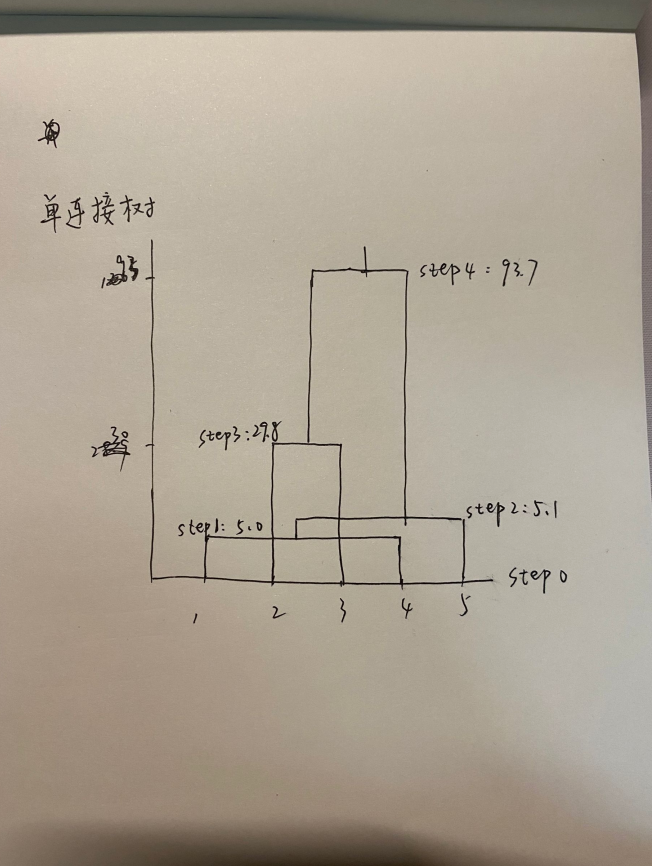
6. *请使用单连接算法描述下列数据是如何进行层次聚类的并画出树状图。*
(10, 8) (70,80) (99,87) (6,5) (5,10) (16分)

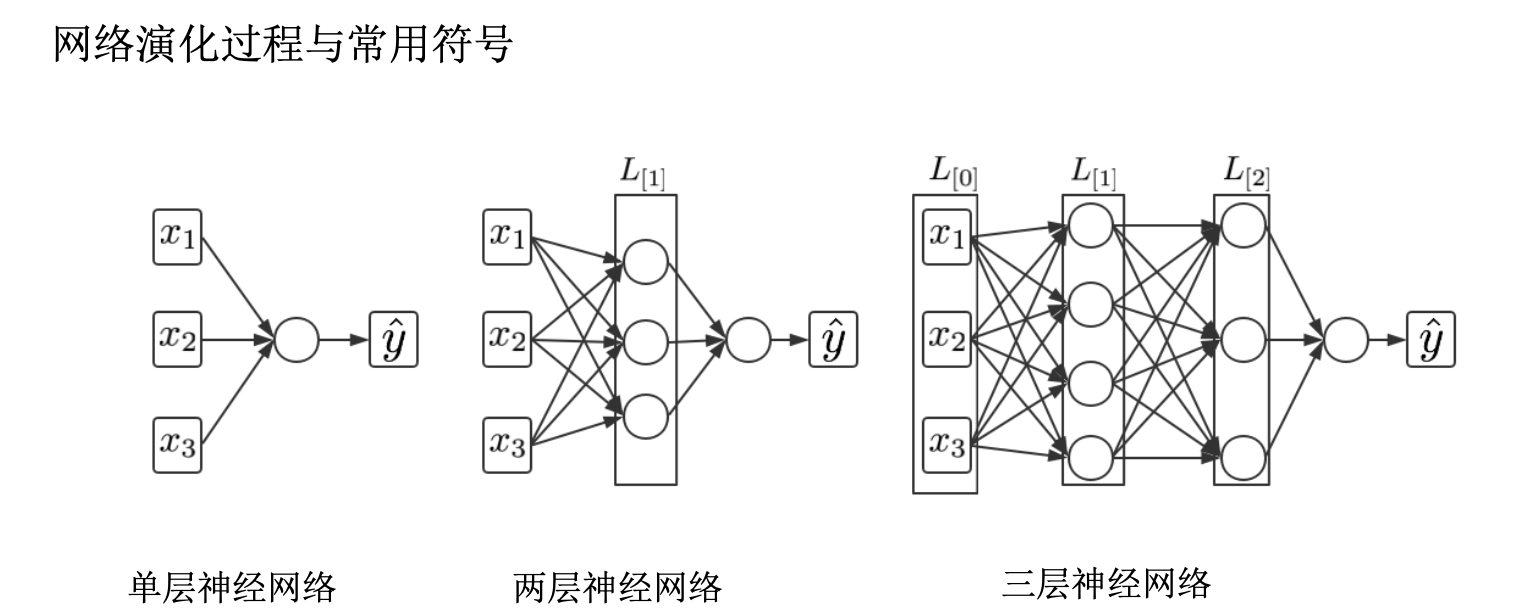
7. *请描述深度学习中前向传递、后项传递和梯度下降含义和作用。(**9**分)*
前向传播 (Forward propagation),指的是:数据从输入层开始,依次经过隐藏层(如果有)最终到达输出层的过程。其中,数据每经过一层传播,其节点输出的值所代表的信息层次就越高阶和概括。节点中输出的值是通过与其相连的前一层中所有的节点输出值的加权求和处理后的结果。
反向传播是计算损失函数对神经网络这个函数中的不同层中参数的偏导数的过程。就是对前向传播产生的结果进行纠正,并把权重参数等进行更新。
梯度下降就是寻找优化参数的方向,对得到的偏差,往哪个方向对参数进行优化。它利用梯度信息,通过不断迭代调整参数来寻找合适的目标值